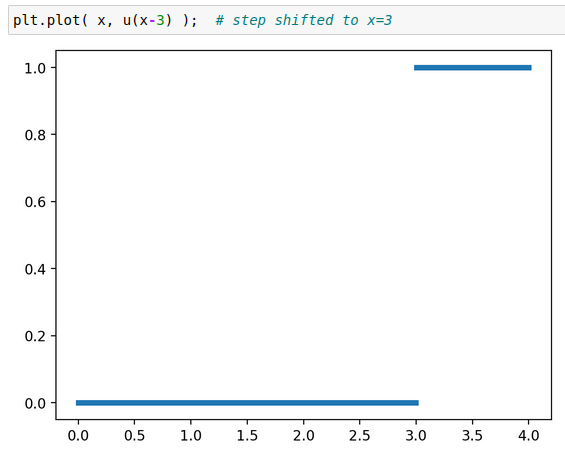
Lab 11: Building functions with the Heaviside step function

Friday, April 25, 2025

The Laplace transform method is useful for solving differential equations with discontinuous or non-smooth forcing.

In order to use it, you'll need to come up with formulas for such forcing in terms of the Heaviside step function. We'll call it "u", and u(x) is 0 for x < 0 and 1 for x ≥ 0.

See if you can obtain formulas in terms of u for the following functions

which have discontinuities and/or breaks in their slope.

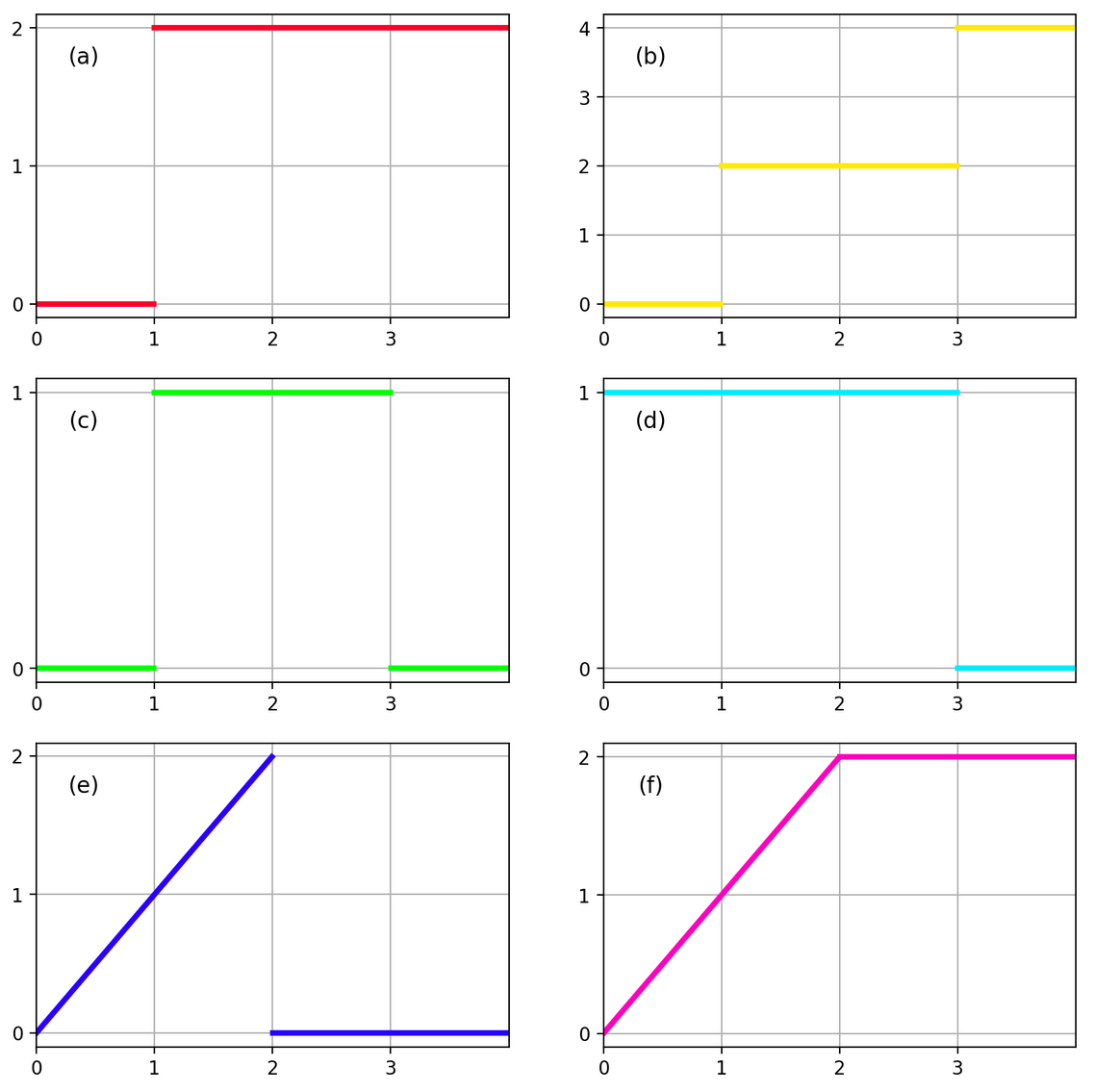
It's best if you can do this just by thinking with pencil and paper, but if you'd like to check your formulas, you can use this code to plot your formulas:

from resources306 import *
%config InlineBackend.figure_format = 'retina'
def heaviside(x):
         y = 0.5 * (np.sign(x) + 1)
         y[:-1][np.diff(y) >= 0.5] = np.nan  # break the line where the jump is
         return y
u = heaviside  # shorthand
x = np.linspace(0,4,1000)  # assume we're interested in x between 0 and 4

which you can use as follows: