1.1 Differential Equations and Mathematical Models

Meaning of DE, solution, example of verifying solution: y’ = x − y, y = ce^− x + x − 1

Python plotting a function, plotting solution families

Modeling and scope: asteroid, smoke, derive predator-prey system

general single 1st order DE, order

1.2 [Omit] Integrals as General and Particular Solutions

1.3a Slope Fields and Solution Curves, Existence and Uniqueness

slope field class exercise and photo dy/dt = (y-t)/2, -2<=t<=5, 0<=y<=6.

slope field code, solutions, initial conditions

matching exercise: autonomous, no-y, nullclines, symmetries

Related lab.

1.4 Separable Equations and Applications

An analytical method for finding solutions

separable: examples of separable and non-separable

y’ = (t)/(y²), y(0) = y₀

Python plot of solutions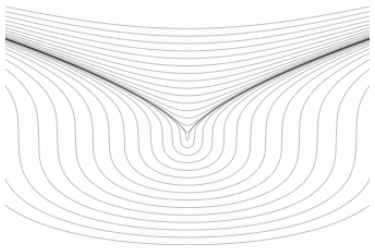

Toricelli, general, cylinder special case - separable (parabolic solution)

1.3b Existence and Uniqueness

E/U Theorem

IVP with at least 2 solutions y^′ = y^2 ⁄ 3 y = 0 and y = (t ⁄ 3)³

f(x, y) = y^2 ⁄ 3, y(0) ≠ 0

Contrast f(x, y) =  − ky

Caution: blow up in finite time f(x, y) = y²

1.5 Linear First-Order Equations

Another class susceptible to analytical solution

y' = P(x)y + Q(x)

integrating factor

examples emphasizing P, Q not necessarily linear

nonexamples

Solution method: integrating factor

Example (x² + 1)(dy)/(dx) + 3xy = 6x

Example dy ⁄ dt =  − ky, C14 dating, half-life

separable/linear venn diagram

1.6 [Omit] Substitution Methods and Exact Equations

2.4 Numerical Approximation: Euler’s Method

Euler's method idea (works even for nasty equations)

Example y' = (x+y)/5, y(0)=2, h=1/2, 2 steps.

Errors - h not too large, local error ~ h^2, ~1/h steps, global error ~h,

interactive demo

error estimation based on global error ~ Ch

Related lab

2.1 Population Models

Malthus and logistic

2.2 Equilibrium Solutions and Stability, Phase Line

Autonomous equations

Qualitative analysis

E/U: translates, no crossing or touching, no up-then-down or vice-versa, 3 allowed behaviors

the phase line as more compact graphical representation | dot for each equil | arrow for sign of y' on each subinterval example logistic

example dy/st = y^2(y(1+y)-2)

classification of equilibria and test for their stability

dependence on parameters, bifurcation

bifurcation: qualitative change in structure of solutions

parameters, coffee cooling dT/dt = k(R-T)

bifurcation diagram as stack of phase lines, example dy ⁄ dt = y² − 2y + μ

calculation of bifurcation point

Related Lab: fishing

2.3 Acceleration–Velocity Models

No new concepts. Just assign a problem or two.

2.5 [Omit] A Closer Look at the Euler Method

2.6 [Omit] The Runge–Kutta Method

3.1 Introduction: Second-Order Linear Equations

A(x)y'' + B(x)y' + C(x)y = F(x)

non/homogeneous, associated homogeneous eqn

mass with restoring force and friction

superposition for homogeneous equations

E/U for linear equations y'' + p(x)y' + q(x)y = f(x), y(a)=y0, y(b)=v0

linear independence of functions on an interval, wronskian

general solution of homogeneous equation, proof

constant coeffs homogeneous equation, characteristic equation

solution in distinct real roots case

solution in repeated roots case

3.2 General Solutions of Linear Equations [of order greater than 2]

Omit all except general solution on nonhomogeneous equation, particular solution

3.3 Homogeneous Equations with Constant Coefficients

Omit higher-order equations.

Complex-valued functions, Euler's formula

Complex roots case

3.4 Mechanical Vibrations

free undamped motion, amplitude, frequency, phase angle / time lag

free damped motion, overdamped, critical damping, underdamped, pseudofrequency,

3.5 Nonhomogeneous Equations and Undetermined Coefficients

flexible guess

duplication

Omit variation of parameters?

3.6 Forced Oscillations and Resonance

undamped forced oscillation, beats, resonance

damped forced oscillation, transient solution, sympy calculation of amplitude vs w

3.7 [Omit] Electrical Circuits

3.8 [Omit] Endpoint Problems [BVPs] and Eigenvalues

4.1 First-Order Systems and Applications

several numbers to specify state

J&M, solution

rabbits and foxes, no analytical solution, but ...

4.2 [Omit] The Method of Elimination

4.3 Numerical Methods for Systems

vector notation (not matrices yet)

vector/direction field, metaphor of the parking lot

Python vector field, example: ?

Euler's method

example: rabbits and foxes

Python demo

[6.1 Do qualitative analysis here as motivation??]

5.1 Matrices and Linear Systems

linear system, matrix representation via product

product definition, distributivity over addition, scalar multiplication, non-commutativity

differentiation

general linear equation dx ⁄ dt = P(t)x + f(t)

what a solution is, existence if P, f continuous on some open I for any IC

associated homogeneous equation, superposition (c_i) theorem, proof, example

linear (in)dependence definition

Wronskian determinant, theorem about solution on open interval if P continuous, example

general solution in terms of n linearly independent solutions on open I, P continuous

existence of linearly independent set via IC standard basis

nonhomogeneous equations: theorem, complementary function aka particular solution

5.2 The Eigenvalue Method for (Constant-Coeffficient) Homogeneous Systems

some vector field pictures

straight-line solutions? need Av=lambda v and then goes as e^{lambda t}

eigenvalues and eigenvectors of matrices, need det A-lambda I = 0, characteristic equation

distinct real eigenvalues, 2D example picture, 3 Great Lakes example

graphical demo of linear combination?

complex eigenvalues, 2D example with picture, 3 brine tanks example

Python sympy computation of eigenvalues and eigenvectors

5.3 A Gallery of Solution Curves of (mostly 2D) Linear Systems

5.4 [Omit] Second-Order Systems and Mechanical Applications (project?)

5.5 Multiple Eigenvalue Solutions

generalized eigenvectors [omit if pressed for time]

5.6 [Omit] Matrix Exponentials and Linear Systems

5.7 [Omit] Nonhomogeneous Linear Systems

6.1 Stability and the Phase Plane

Not much in this chapter except def of asymptotic stability - move that to next section

Swap in material from 6.3: Nullclines and equilibria of 2D nonlinear autonomous system, example rabbits and foxes [NOTE: all of this can be done before almost all of Ch 5!]

qualitative phase portrait

competing species model, dx ⁄ dt = 2x(1 − x ⁄ 2) − xy dy ⁄ dt = 3y(1 − y ⁄ 3) − 2xy

Related lab

6.2 Linear and Almost Linear Systems

linearization of autonomous nonlinear 2D system at an equilibrium point, Jacobian

stability theorem

6.3 Ecological Models: Predators and Competitors

examples 6.4 Nonlinear Mechanical Systems ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~

pendulum, damped and undamped

6.5 [Omit] Chaos in Dynamical Systems

8.1 Introduction and Review of Power Series

Taylor series of a function, power series

python picture, radius of convergence

analytic at a point: def, examples, combinations

examples: 1 ⁄ (xcosx), |x|, x^4 ⁄ 3, exp( − 1 ⁄ x²)

derivatives by repeated differentiation of DE, example: Airy's eqn y'' -xy = 0, y(0) = a0, y'(0)=a1

power series method: termwise diff, identity principle

example y'+3y=0, recurrence relation, index shift

radius of convergence theorem

example y'' + y = 0

8.2 Series Solutions Near Ordinary Points

linear 2nd order homogeneous DE: A(x)y'' + B(x)y' + C(x)y = 0, y'' + P(x)y' + Q(x)y = 0

ordinary/singular point, examples

ordinary point theorem, including radius of convergence bound

translated series to initial point

less simple types of recurrence relations

omit Legendre equation?

with sympy?

8.3 Regular Singular Points

regular singular point: def

method of Frobenius: Frobenius series, equidimensional equation, indicial equation, exponents

case of integer difference of exponents

with sympy?

8.4 [Omit] Method of Frobenius: the Exceptional Cases

8.5 [Omit] Bessel's Equation

8.6 [Omit] Applications of Bessel Functions

7.1 Laplace Transforms and Inverse Transforms

DE to algebraic equation

def, examples: 1, exp(9t), exp(at), step(Heaviside) u_b(t), t^n

linearity

inverse transform by table

piecewise continuous functions via steps

existence/uniqueness [lightly]

7.2 Transformation of Initial Value Problemss

transform of derivative, theorem, formula by integration by parts

solution of IVP: y'=13y, y(0)=8. y' = 2y + 3e^{-t}, y(0)=4.

transform of higher derivatives, sin, cos, 2nd order IVP example

linear system (constant coefficients)

transforms of integrals

7.3 Translation and Partial Fractions

partial fractions

translation on s-axis

7.4 Derivatives, Integrals, and Products of Transforms

convolution: def, transform

differentiation of transform

integration of transform

7.5 Periodic and Piecewise Continuous Input Functions

translation on t-axis

integrodifferential equation

transform of periodic function

7.6 Impulses and Delta Functions

delta functions, transform

transfer function, weight function, Duhamel's principle