Instructor

John Ringland ringland@buffalo.edu

Class times and places

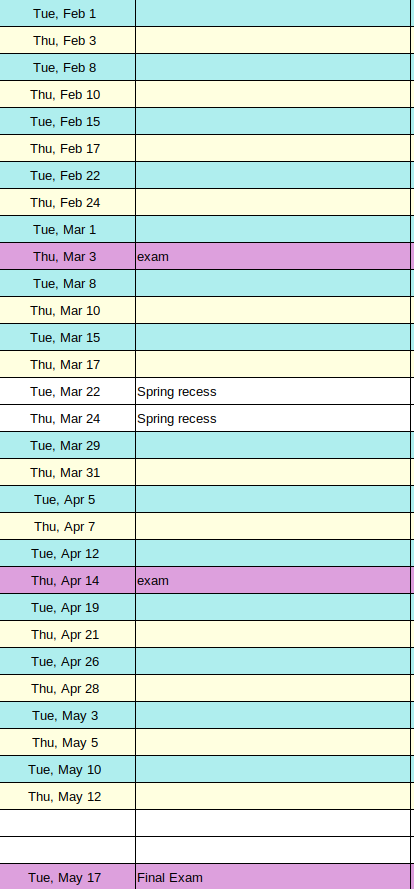
Lecture: Tuesdays and Thursdays, 11:00AM-12:20PM.

Lecture location: Baldy 127 on Tuesdays, 205 Math Bldg on Thursdays.

Office hours: Math Bldg Room 206. Times TBD.

Discord invite: https://discord.gg/wTQenP3Y

Computing

The course will be quite hands-on, and you'll be writing quite a bit of code. The language you will use is Python (not Matlab). Please download and install the Anaconda distribution of Python 3.9, if you haven't already. This includes Jupyter notebook, a useful coding environment.

The goal is that you'll emerge from the class with not only theoretical understanding but also practical skills.

Anaconda distribution of Python 3.9 download

Jupyter and Python Basics

Computing with Numpy

Numpy for former Matlab users

Course resources

Website: http://blue.math.buffalo.edu/538

Homework

Weekly starting 2nd week. Due at 11:59pm Fridays. You will upload your work either to UBlearns or to Gradescope, depending on the content.

Exams

There will be 2 in-class midterm exams (80 minutes each) and a comprehensive Final Exam (3 hours).

Project

An exercise longer than homework problems. Several options to choose from.

Grades

Homework 20%

Class participation 10%

Midterm 1 20% Thursday March 10

Midterm 2 20% postponed to Tuesday April 19

Project 10% Project submission date: 11:59pm Tuesday, May 10.

Final Exam 20%. Tuesday May 17. (11:45am-2:45pm, comprehensive.) This exam also serves as a Qualifying Exam for those in the Math PhD program.

Coding

The programming language you'll be using is Python (not Matlab).

Academic integrity

UB's Academic Integrity policies will be enforced. The overarching principle is that the work you turn in will be entirely your own work.

Accessibility

If you need accommodations due to a physical or learning disability please contact the UB Accessibility Resources Office to make appropriate arrangements.

Content

The course will be focused on numerical methods for solving differential equations.

• ODE: initial and boundary value problems
• PDEs

Textbook

• Ackleh et al., Classical and Modern Numerical Analysis (same text as for MTH 537 in Fall)

Source materials will aslo come from the following, and others:

• Golub & Ortega, Scientific Computing and Differential Equations
• Ames, Numerical Methods for Partial Differential Equations
• Sauer, Numerical Analysis (2e)
• Trefethen, Spectral Methods with M-----